FTQC量子资源计数器
为什么需要FTQC资源计数器
在NISQ(Noisy Intermediate-scale Quantum)设备上,衡量一个算法消耗的资源是非常直观的。通过算法使用的门的数量,物理比特的数量,电路的深度,物理硬件的各种错误率与保真度就可以大致的评估一个算法。但在FTQC(Fault Tolerant Quantum Computing)上事情却复杂一些。最关键的不同在于FTQC使用纠错码的方式通过设置更多冗余的物理比特来降低错误率,具体的细节可以参考之前的博文。
但对应的,在FTQC上,量子电路使用的比特数量是编码后的逻辑比特的数量而非真实的物理比特数量。对于每一个逻辑比特,FTQC都要使用数十到数百不定的物理比特来编码它。再加上有一些特殊的操作,比如对于surface code来说是T gate,每一个都需要额外的物理比特来实现。这让FTQC上的资源统计与评估变得没有那么直观。所以在FTQC上,我们需要一套特殊的机制来实现对于算法使用资源的衡量。
运行时间
在FTQC上,运行时间是相对容易统计的。首先我们需要知道的是一轮量子纠错码纠错所需要的时间。这里使用表面码作为样例,对于每一轮纠错,运行在量子设备上的电路为:
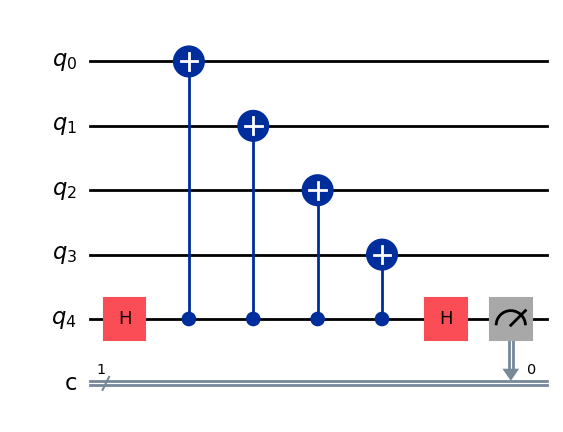
由此可见,一轮纠错所需要的时间是两个单比特门的时间加上四个双比特门的时间。同时,为了减少测量错误,FTQC通常每一个门都会执行多轮纠错来降低错误率。这样,总运行时间的估算公式就可以得到了:
$$
T_{total} = d_{rounds} * depth * (2 * T_{one} + 4 * T_{two})
$$
物理比特数量
估算物理比特数量则是一个更加复杂的问题,在基于表面码的量子纠错机制中,物理比特的数量可以分为两个部分统计:
- 电路本身逻辑比特所用的物理比特的数量。
- 特殊门工厂所使用的物理比特的数量。
码距
一个纠错码的码距为$d$,等同于这个纠错码可以纠正$\lfloor\frac{d-1}{2}\rfloor$个错误。在表面码里,码距为$d$的表面码需要用$2d^2 - 1$个物理比特实现一个逻辑比特。所以纠错码使用多少码距决定了一个逻辑比特对应多少物理比特以及这个逻辑比特的错误率是多少。一般来说,$d$越大,需要的物理比特越多,纠错性能越好。
从更低的错误率来说,码距当然是越高越好,但是物理量子比特数量是宝贵的资源。所以在FTQC资源计数器里,码距被设定为是“满足整个算法的期望错误数量<1”的最小值。资源计数器通过stim模拟+倍增+二分的方法,来确定$d$的值具体是多少。
电路物理比特数量
确定码距之后,电路物理比特数量的公式就很简单了:
$$
N_{pqubits} = N_{lqubits} * (2 * d^2 - 1)
$$
特殊门工厂物理比特数量
这个值是统计FTQC使用资源的最后一块拼图。对于任何一种纠错码来说,想要实现模拟所有量子比特门的操作,就必然会存在一个门是无法直接实现的。对于表面码来说这个操作就是T-gate。普通的表面码只能实现Clifford门的直接模拟,对于非Clifford门,表面码必须引进T Gate来进行近似模拟。目前在表面码里实现T-Gate的方法是T-Factory。每个T-Factory可以生成一个魔法量子态,让这个量子态和逻辑比特纠缠就可以实现近似T-Gate的操作。
对于每一个T-factory来说,它需要15个逻辑比特,所以统计T-factory所需要的物理比特的数量就需要知道T-Factory的数量。而T-Factory的数量由T-Gate在电路里所需的频率决定。对于每个T-Factory,它需要生成一个魔法量子态的时间是$T_{Tstate}=d_{rounds} * 10 * (2 * T_{one} + 4 * T_{two})$,所以T-Factory生成魔法量子态的速度为$T_{freq}=\frac{1}{T_{Tstate}}$。用电路所需的T Gate的频率除以T Factory生成的速度向上取整,就可以得到T Factory所需的数量:$N_{TFactory} = \frac{\frac{N_{TGate}}{T_{Total}}}{T_{freq}}$
最后,T Factory所需的物理比特数量即为$N = N_{TFactory} * 15 * (2 * d^2 - 1)$
总结
至此,所有FTQC量子算法所需要的资源都已经统计结束,具体的代码实现可以参考:
https://github.com/melody0123/QAOA4FTQC