FTQC Resource Estimator
Why We Need an FTQC Resource Estimator
On NISQ (Noisy Intermediate-scale Quantum) devices, measuring the resource cost of an algorithm is very intuitive. By counting the number of gates the algorithm uses, the number of physical qubits, the circuit depth, and taking into account various hardware error rates and fidelities, one can roughly estimate an algorithm’s performance. However, in FTQC (Fault-Tolerant Quantum Computing) things become more complex. The most significant difference is that FTQC uses error-correcting codes with extra redundant physical qubits to suppress errors—see my previous blog post for details.
Consequently, in FTQC the “qubit count” refers to the number of encoded logical qubits, not the actual physical qubits. Each logical qubit typically requires dozens to hundreds of physical qubits for encoding. Moreover, certain special operations—such as the T gate in the surface code—demand additional physical qubits to implement. This makes resource accounting in FTQC far less straightforward. Therefore, we need a dedicated mechanism—the FTQC Resource Estimator—to measure algorithmic resource usage accurately.
Runtime
Estimating runtime in FTQC is relatively straightforward. First, we must know the time required for one round of quantum-error-correction (QEC). Using the surface code as an example, each correction round on the device involves the circuit below:
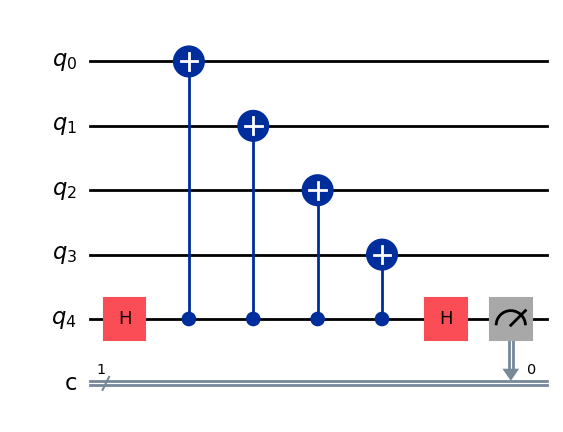
From this, one QEC round takes the time for two single-qubit gates plus four two-qubit gates. Moreover, to reduce measurement error, FTQC typically performs multiple correction rounds per gate. Thus the total runtime can be estimated as:
$$
T_{total} = d_{rounds} \times depth \times \bigl(2,T_{one} + 4,T_{two}\bigr)
$$
Physical Qubit Count
Estimating the physical qubit count is more involved. In surface-code QEC, the total physical qubits consist of two parts:
- Physical qubits for the circuit’s logical qubits.
- Physical qubits for the magic-state factories (e.g., T-factories).
Code Distance
A code’s distance is (d), which determines its ability to correct up to (\left\lfloor\frac{d-1}{2}\right\rfloor) errors. In the surface code, one logical qubit with distance (d) requires (2d^2 - 1) physical qubits. Thus the chosen distance (d) sets both the physical-to-logical qubit ratio and the logical-qubit error rate. While larger (d) yields lower logical error rates, physical qubits are costly. Therefore, the Resource Estimator chooses the minimal (d) that ensures the algorithm’s expected total errors remain below one. This (d) is found via a combination of stimulus simulation, error-rate amplification, and binary search.
Circuit Physical Qubit Count
Once (d) is determined, the physical qubits for the circuit’s logical qubits are:
$$
N_{pqubits} = N_{lqubits} \times \bigl(2,d^2 - 1\bigr)
$$
Magic-State Factory Physical Qubit Count
This completes the resource accounting. In any QEC code, there will be at least one gate that cannot be directly implemented; for the surface code, that is the T gate. Surface-code implementations only natively support Clifford gates, so non-Clifford gates require magic states generated by T-factories. Each T-factory produces one magic state, which, when entangled with a logical qubit, implements an approximate T gate.
Each T-factory itself uses 15 logical qubits, so its physical-qubit cost depends on the number of factories needed. That number is set by the T-gate frequency in the circuit. A single factory’s magic-state generation time is
$$
T_{Tstate} = d_{rounds} \times 10 \times \bigl(2,T_{one} + 4,T_{two}\bigr),,
$$
so its generation rate is (T_{freq} = 1 / T_{Tstate}). Dividing the circuit’s T-gate rate (\bigl(N_{TGate}/T_{total}\bigr)) by (T_{freq}) and rounding up gives
$$
N_{TFactory} = \left\lceil \frac{N_{TGate}/T_{total}}{T_{freq}} \right\rceil.
$$
Finally, the physical qubits for all T-factories are:
$$
N = N_{TFactory} \times 15 \times \bigl(2,d^2 - 1\bigr).
$$
Summary
With the above, the FTQC Resource Estimator has accounted for all key algorithmic resources. For implementation details, see the code at:
https://github.com/melody0123/QAOA4FTQC